Heat seeking kitten

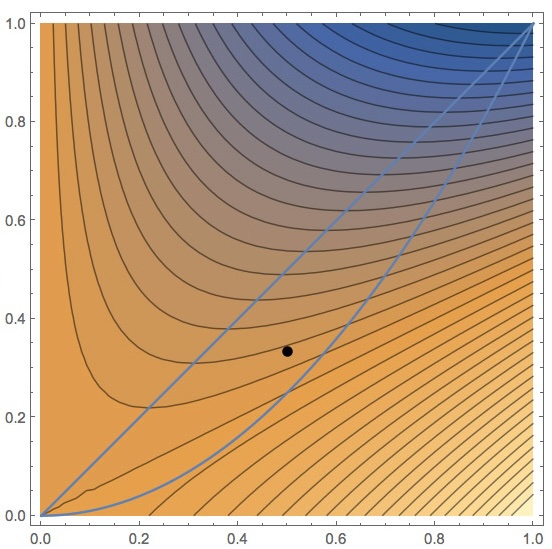Let $T(x,y)=x^2-2xy$ be the temperature at a point $(x,y)$ in the region bounded by the curves $y=x$ and $y=x^2$. (Blue lines on the accompanying contour plot.) Suppose that a kitten is crawling around the region.

1. At $P=(\frac12,\frac13)$ , in which direction should the cat go to cool down as quickly as possible?: Draw a vector on the contour plot indicating the direction. And find the components of the gradient and use it to justify your answer.

   The gradient of $T$ is $$\myv \grad T=\langle T_x,T_y\rangle =\langle 2x-2y,-2x\rangle.$$ When $\langle x,y\rangle=\langle\frac12,\frac13$ we find, $$\begineq \myv \grad T&=\langle 1-\frac23, -1\rangle\\ &=\langle \frac13, -1\rangle\\ \endeq $$ This is the direction of steepest increase! So the direction of steepest decrease should be in the direction of $-\myv \grad T = \color{blue}\langle -\frac13, +1\rangle$.

2. At $P$, in what direction(s) could the kitten go to maintain its current temperature?

   It should move along a contour line, that is to say at right angles to $\myv \grad T \langle \frac13, -1\rangle$. That is, either $\color{blue}\langle 1, \frac13\rangle$ or $\color{blue}\langle -1, -\frac13\rangle$

3. Where is the hottest point inside the region? Mark it on the contour plot. Explain your answer.

   On the boundary at approximately $(0.3,0.1)$: on the blue boundary where the blue boundary is parallel to the nearest countour just outside.

4. If, at $P$, the cat moves in such a way that for each change in its $x$ direction of 2 units, the change in the $y$ direction is –1 unit, find a value for $\frac{dT}{dt}$, the rate of change of the temperature, from the kitten’s point of view. (Give your answer some plausible units).

   The kitten will move in the direction $\myv u = \langle 2,-1 \rangle$. The question is asking for the directional derivative $D_{\uv u} T=\myv \grad T\cdot \uv u$. So a unit vector in the $\myv u$ direction would be $\uv u=\langle \frac2{\sqrt 5},\frac{-1}{\sqrt 5} \rangle$. So, the derivative in the $\myv u$ direction is: $$\begineq \myv \grad T\cdot \uv u &= \langle \frac 13, -1\rangle\cdot \langle \frac2{\sqrt 5},\frac{-1}{\sqrt 5} \rangle\\ &= \frac2{3\sqrt5}+\frac1{\sqrt5}=\color{blue}0.7454\color{black}\text{ degrees C / meter}\\ \endeq $$ Does this make sense? No directional derivative should be greater than the magnitude of the gradient, which is $$|\myv \grad T| = |\langle\frac13,-1\rangle|=\sqrt{(1/3)^2+(-1)^2} =1.05\gt 0.7454.$$ Good! This is a possible slope away from the gradient direction!