Lines [9.5]


Casa Batlló by Antoni, "enemy of the straight line" Gaudí and Josep Maria Jujol.

Vector form of a line

It seems like "two points determine a line" should work in three dimensions as well as in 2-d. But we may have hit a dead end with $y=mx+b$: It's not obvious what the "slope" is in 3-d. It's certainly not a scalar number.

In the preview activity, you became acquainted with a new way of describing a line, that still works in 2-d but generalizes to 3-d more easily. The line that passes through 2 points $P$ and $Q$...


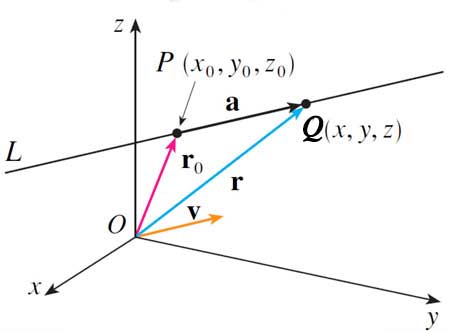
  • $\myvv{OP}=\myv r_0$ is the position vector of a point on the line with tail at the origin, and head at point $P=(x_0,y_0,z_0)$.
  • $\myvv{PQ}\equiv \myv a$ is the difference vector, which runs from $P$ to some other point $Q$, both on the desired line.
  • $\myv v=\langle a,b,c\rangle$ is the direction vector, and it is parallel to $\myv a$.
  • Any vector parallel to $\myv v$ can be expressed as some scalar multiple $t\myv v$ of $v$.

So, using vector addition, we can express the set of points on the line in parametric form (as a function of the parameter $t$) as:

Vector form of a line $$\myv r(t)=\myv r_0 + t\myv v$$

  • If you know any two points on a line, say $P$ and $Q$, you can use the difference vector $\myvv{PQ}$ as your direction vector.
  • Even in 2-d, we could use this form to describe vertical lines, e.g. using $\myv v=\langle 0,1\rangle$, something we can't do with $y=mx+b$.

Do Activity 9.5.2. Parallel lines?

The parametric equations of a line

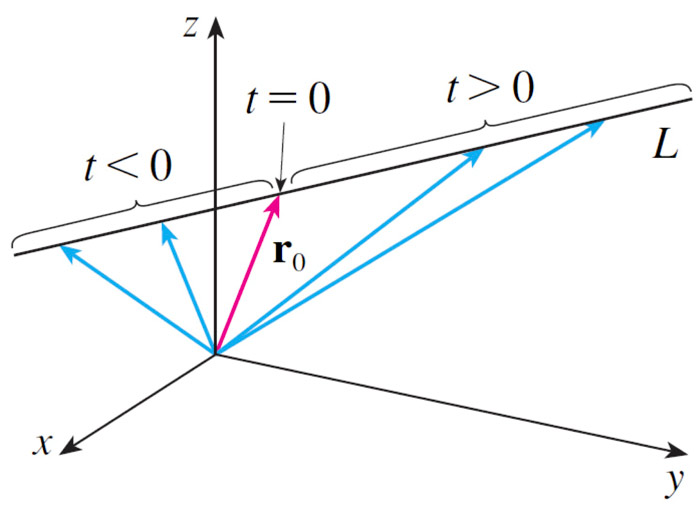$$\begineq \myv r(t) &= \myv r_0 + t\myv v \\ &= \langle x_0,y_0,z_0\rangle+t\langle a,b,c\rangle \\ \langle x(t), y(t), z(t)\rangle&= \langle x_0+ta, y_0+tb, z_0+tc \rangle .\endeq $$

We know that a 3-d vector equation is really *3* equations. In order for two vectors to be equal, their $x$-, $y$-, and $z$-components must each be equal. The three equations here are:

Parametric equations for a line $$x(t)=x_0 +at;\ \ y(t)=y_0 +bt;\ \ z(t)=z_0 +ct$$

Each of these 3 can be solved for $t$, e.g. $\frac{x(t)-x_0}{a}=t$. We'll have three expressions each equal to $t$, so we can set them mutually equal:

Symmetric equations of a line $$\frac{x-x_0}{a}=\frac{y-y_0}{b}=\frac{z-z_0}{c}.$$

  • Notice that $a$, $b$, $c$ are the components of $\myv v$, the direction vector parallel to the line $L$.
  • These are something like the point-slope form of the equation of a line in 2-d. Indeed, the first two equations for a 2-d line can be arranged like this: $$\frac{y-y_0}{x-x_0}=\frac ba \equiv m.$$

    A 9.5.3 Is a point on the line?

    Example

    Consider two lines: $$\nonumber x=1+t;\ \ y=-2+3t;\ \ z=4-t$$ and $$\nonumber x=2s;\ \ y=3+s;\ \ z=-3+4s$$

    Do they intersect?

    Solution: If they intersect at some common point (x,y,z), then that point should be a simultaneous solution in $s$ and $t$ to these three equations: $$1+t=2s;\ \ -2+3t=3+s;\ \ 4-t=-3+4s$$

    Those same two lines: $$\nonumber x=1+t;\ \ y=-2+3t;\ \ z=4-t$$ and $$\nonumber x=2s;\ \ y=3+s;\ \ z=-3+4s$$

    Are the lines parallel?

    Solution: Re-arrange the equations into the form of the symmetric equations (solve each equation for $t$...or for $s$...) to find the components (denominators) of a vector parallel to each line.

    Lines which are not parallel to each other, and do not intersect are called skew lines.

    To do

    • Lines in the plane

    Image credits

    vgm8383