Planes [9.5]

Ben Tuinman on Flickr

How2 specify a line in $\mathbb{R}^3$?...

$$\myv r(t)=\myv r_0+t\myv v$$ One point and one vector will do it.

What do we need to uniquely specify a plane in $\mathbb{R}^3$? We shall see that one point and one vector will also be enough to uniquely specify a plane!

Planes

A plane can be determined by

• a point $P_0$ in the plane and
• a normal vector, $\myv n$, which is orthogonal (normal) to the plane.

In pictures...

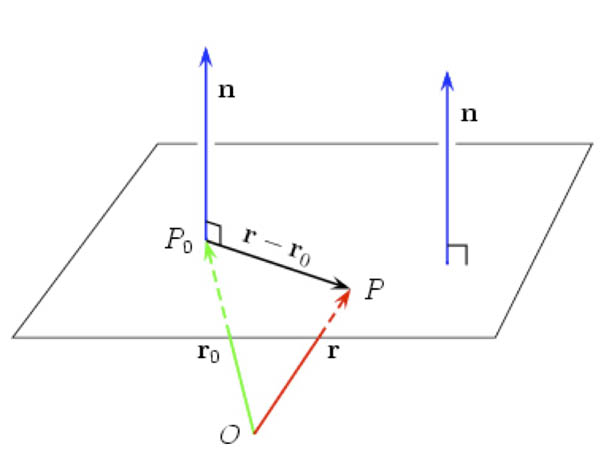
• $\myv r_0=\langle x_0, y_0, z_0 \rangle$ is a vector pointing at $P_0$.
• $\myv n = \langle\color{blue}a, b, c\color{black} \rangle$ is the normal vector.
• $\myv r=\langle x,y,z\rangle$: Some point in the plane, which must satisfy the condition that $\myv r -\myv r_0$ is perpendicular to $\myv n$:

With these definitions:

Equations of a plane: $$\begineq \text{"vector" eq:}\ \ \ \ 0&=\myv n \cdot (\myv r-\myv r_0)\\ &=\langle \color{blue}a,b,c\color{black} \rangle \cdot \langle x-x_0,y-y_0,z-z_0\rangle\\ \text{"scalar" eq:}\ \ \ \ 0&=\color{blue}a\color{black} (x-x_0)+\color{blue}b\color{black}(y-y_0)+\color{blue}c\color{black}(z-z_0)\rangle\\ \endeq $$

Pushing the equation above one step further, let's expand the products and add up all the constant terms calling their sum $k=\myv n\cdot\myv r_0$: $$\begineq ax_0+by_0+cz_0&=ax+by+cz\\ k&=ax+by+cz \endeq $$

So that if you see an equation for a plane such as: $$56=7x-3y+2z,$$ You can just read off the components of a normal vector to the plane as: $$\myv n=\langle 7,-3,2 \rangle.$$

Do Problem 7 - Angle between planes.

Example 1a: Equation of a plane from 3 points

Alternatively, any 3 points define a unique plane. This desmos/3d graph calculates a normal vector from 3 points, and uses it in the form above (see cell 9!) to graph a plane.

Example 1b: Scalar equation

Returning to the 3 points example. What was that normal vector? Let's work out the scalar equation for that plane...

You can carry out the cross product to find $\myv n$. But in this new example, you may see how desmos/3d can do it for you...

Once we know the normal vector $\myv n=\langle a,b,c\rangle$, we know that the equation for the plane can be written as $$ax+by+cz = k.$$ We can find $k$ by using a slider, once we have $\myv n$...

Is there an easy way to find $k$ exactly?

Yes, we just substitute the coordinates $R_0 =(x_0,y_0,z_0)$ of a point in the plane that we know, into the equation above to find $k$.

[Hey! This looks as if we're taking the dot product of (the position vector of the point in the plane) $\cdot$ (the normal vector), that is $\myv r_0\cdot\myv n = k$. Well, yes... It turns out that if we normalized our unit vector to $\uv n = \myv n/ n$ that $\myv r_0\cdot\uv n$ is the closest distance from the origin to the plane.... ]

Example 2

A plane intersects the $x$-, $y$-, and $z$-axes at the points shown. Find the equation of the plane.

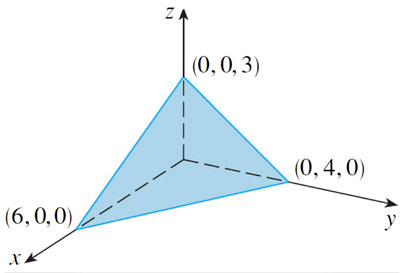
First find the normal to the plane.
[Find two vectors that are in the plane, and then take their cross product.]

Then find the equation for the plane. [Take as $\myv r_0$ any of the three points shown.]

Find the surface normal:
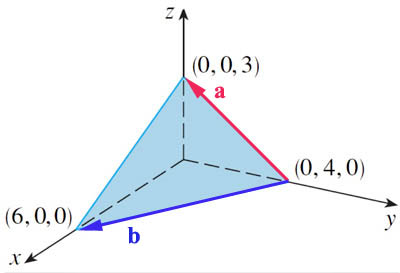$\myv a=\langle 0,-4,3 \rangle$
$\myv b=\langle 6,-4,0 \rangle$
$\myv a \times \myv b=12\uv i+18\uv j+24\uv k$

Let's take for the normal vector $\frac16$ of the the vector above (just because we'll have smaller numbers to keep track of...): $$\myv n=2\uv i+3\uv j+4\uv k =a \uv i + b \uv j +c \uv k$$

Picking $(0,4,0)$ as the point in the plane, then the prescription above is... $$\begineq 0 &=a(x-x_0)+b(y-y_0)+c(z-z_0)\\ &=2(x)+3(y-4)+4(z) = 2x+3y-12+4z\\ \endeq$$ So, the equation for the plane can be written as: $$2x+3y+4z = 12.$$ where a normal vector to the plane was $\myv n=\myc{2,3,4}$.

Notice that when the equation for a plane is written in this form that you can read off the components of the normal vector from the coefficients of $x$, $y$, and $z$!