Cylindrical and Spherical Coordinates [11.8]

Polar coordinates (2-d)
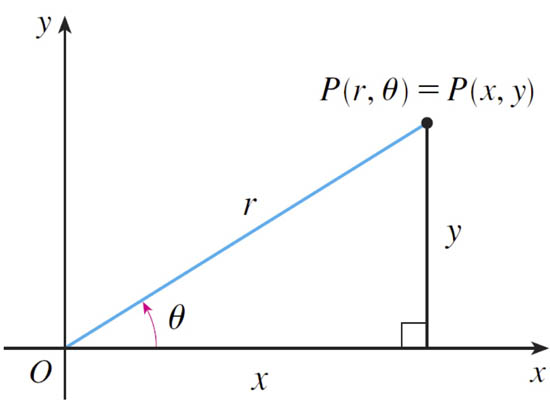
$(x,y)\to (r,\theta)$: $$r^2=x^2+y^2;\ \ \ \tan \theta = \frac yx.$$
$(r,\theta)\to(x,y)$: $$x=r\cos\theta;\ \ \ y=r\sin\theta.$$
Cylindrical coordinates (3-d)
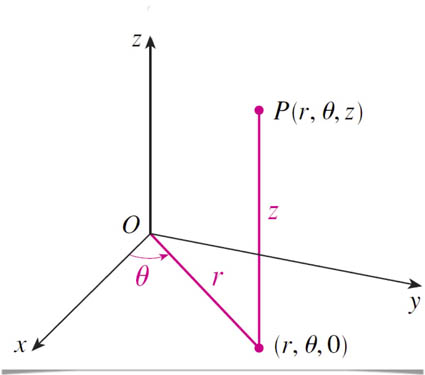 Polar coordinates in the $x-y-$plane, plus $z$ which is the same in cylindrical and Cartesian coordinates.
Polar coordinates in the $x-y-$plane, plus $z$ which is the same in cylindrical and Cartesian coordinates.
- Cylindrical Coordinates (*.nb)
"Cylindrical Coordinates" from the Wolfram Demonstrations Project,Contributed by: Jeff Bryant
For example
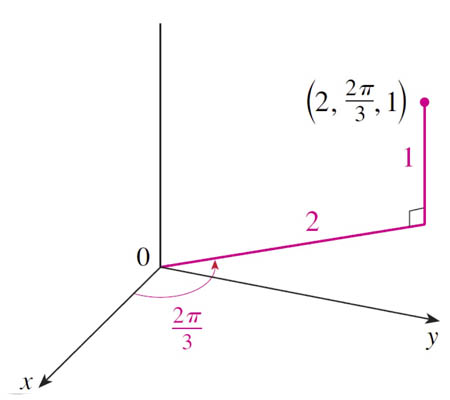 $(r,\theta,z)=(2,\frac{2\pi}{3},1)$:
$(r,\theta,z)=(2,\frac{2\pi}{3},1)$:
- $x=r\cos\theta = 2 (-\frac 12)=-1$
- $y=r\sin\theta=2 (\frac{\sqrt{3}}{2})=\sqrt 3$
- $z=z=1$
N.B. If an angle measure doesn't explicitly have the degree mark, ${}^o$, it's in radians!
All the computer / math packages I've used, work primarily in radians.
Converting $$\pi \text{ radians} = \frac 12\text{ rotation} = 180^o.$$ So, for example, $\pi/6$ radians... $$\frac{\pi}{6}\text{ radians}\cdot \frac{180^o}{\pi\text{ radians}}=\frac{180^o}{6}=30^o.$$
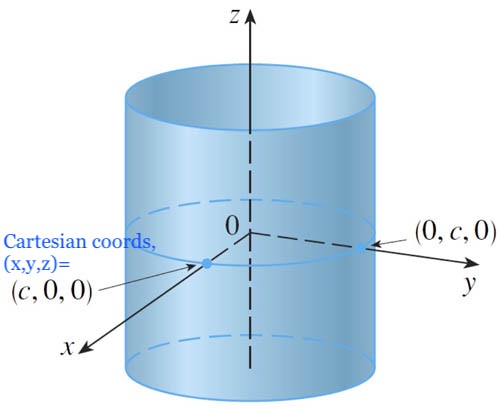
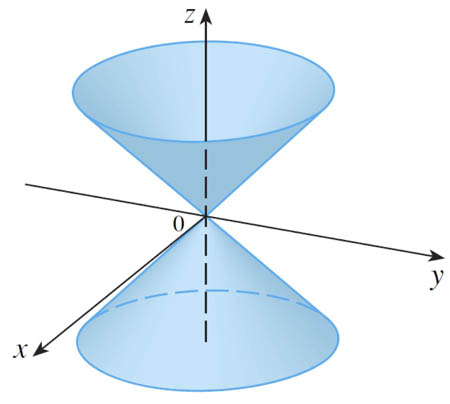
Some surfaces
...which are easily specified in cylindrical coordinates
$$r=c\nonumber$$
$$r=z\nonumber$$
Spherical coordinates (3-d)
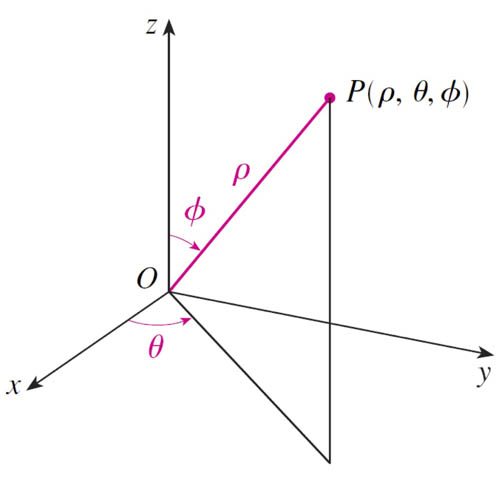
- $\rho$ - "rho" - radial distance
- $\theta$ - "theta" - azimuthal angle
- $\phi$ - "phi" - polar angle
This is the convention used by publishers of calculus textbooks, and Wolfram's own MathWorld website.
However, physicists, engineers, Mathematica (in some contexts), MatLab, and even applied mathematicians use a different convention, where $\theta$ is the polar angle and $\phi$ is the azimuthal angle.
:-<
In this course, we'll use the calc-textbook convention:
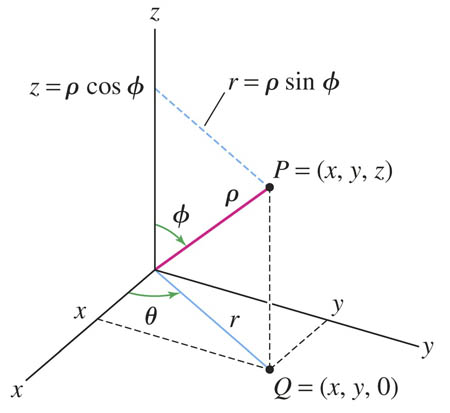
Use $r\equiv$ projection of $\rho$ into $x-y-$plane=$\rho\sin\phi$:
- $x=r\cos\theta = \rho \sin\phi \cos\theta.$
- $y=r\sin\theta = \rho \sin\phi \sin\theta.$
- $z=\rho \cos \phi.$
$(x,y,z)\to(\rho,\theta,\phi)$
- $\rho^2 = x^2+y^2+z^2.$
- $\tan\theta = \frac yx.$
- $\cos\phi =\frac z\rho.$
Discuss limits of angles phi and theta.
Example
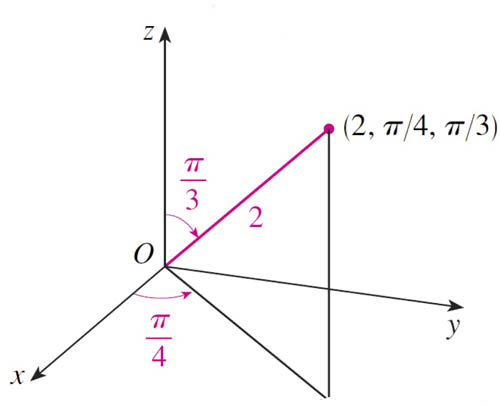
$(\rho,\theta,\phi)=(2,\pi/4,\pi/3) \to (x,y,z)$?
- $z=\rho \cos \frac{\pi}{3} = 1$
- $r=\rho \sin \frac{\pi}{3} = \sqrt 3$
- $x=r \cos \frac{\pi}{4}=\sqrt{3/2}\approx 1.22$
- $y=r \sin \frac{\pi}{4}\approx 1.22$
Surfaces in spherical coordinates
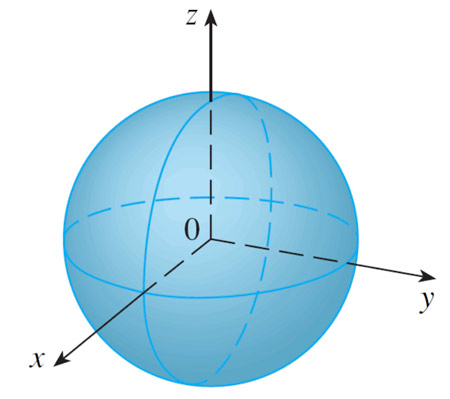
$$\rho=c$$
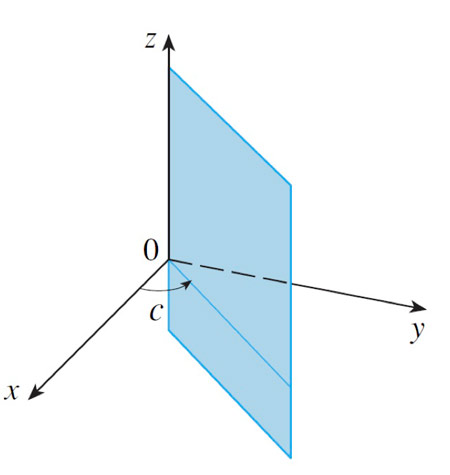
$$\theta=c$$
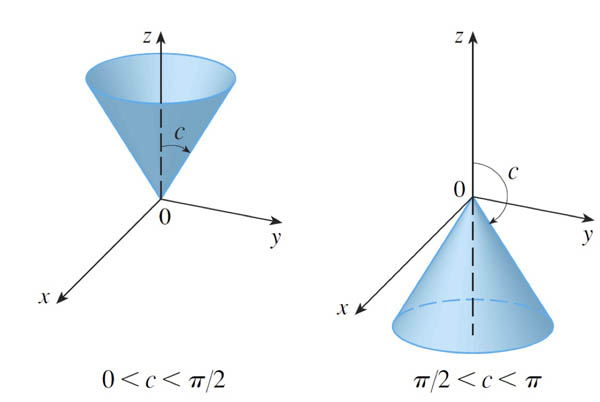
$$\phi=c$$
- Animation at mathinsight.org
- In GeoGebra, you can plot a Surface( [x function], [y function], [z function], .....) parametrically in terms of two parameters. For example, a sphere.
- Spherical Coordinates (*.nb)
"Spherical Coordinates" from the Wolfram Demonstrations Project,Contributed by: Jeff Bryant
To do
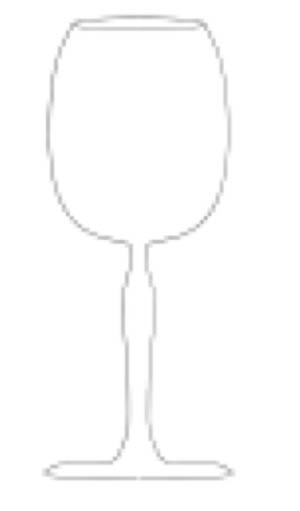 Describe me:
Describe me:
Come up with an expression (in cylindrical coordinates) to approximately describe the surface of a goblet:Find an equation (well, actually several), $r(z),$ such that if you rotate the graph about the $z$ axis you'll get a shape that resembles a goblet . You'll actually need one equation for each vertical segment of the goblet. And then, if you don't specify $\theta$, it can take on any possible value. This is produces a "surface of rotation".
To actually code this in Geogebra, you'll use the Surface(...) function, which allows you to specify a set of points, using two parameters.
For example, a crude base to the goblet, might be to specify a straight cross section, (I'm thinking in millimeters): $$r(z)=10-10z\ \text{ for }\ 0\lt z \lt 1$$ and then "rotate" this graph, by letting $\theta$ run from 0 to $2\pi$.
In the $(x,y,z)$ coordinates that Geogebra wants, you'd have: $$\nonumber x(\theta,z)=r(z)cos(\theta);$$ $$\nonumber y(\theta,z)=r(z)sin(\theta);$$ $$\nonumber z(\theta,z)=z$$
Here's the example.
You'll plot this in today's lab
(Further detail about how to "hand in" this assignment in the "Lab 04" notebook file for today on CoCalc.)