Thermal energy / Heat / Mixing

Lab 6

See the revised 6-HeatPulses.pdf lab if I asked you to re-calculate the size of your heat steps.

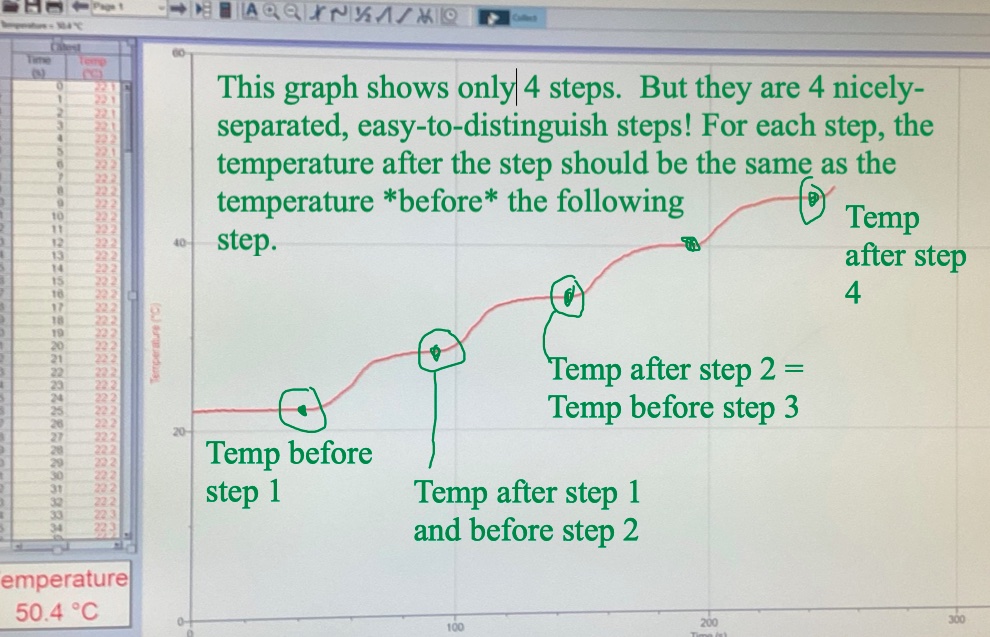
In Lab 6 We used this expression for the thermal energy (or heat energy), $Δ Q$ (in calories) needed to raise the temperature of some water: $\begin{matrix} (1) & Δ Q = m c Δ T \end{matrix}$ where...

$m$ [grams] - the mass of liquid
$Δ T$ [ $^{o}$ C] - the change in the temperature of the liquid
$c$ [calories /( $^{o}$ C $\cdot$ grams) ] - the "heat capacity" of the liquid.

The "heat capacity" of a liquid is the number of calories it takes to raise the temperature of 1 gram of a substance by 1 degree C. For example, $c_{water} = 1 cal / (^{o} C \cdot grams)$ .

The goal of adding heat pulses to antifreeze (which is "Ethylene Glycol") is to use the measurements to estimate the heat capacity of something other than water. In part e you're asked to do this:

The text highlighted in yellow is the definition of the heat capacity, $c$ . So, start by using algebra to solve our thermal energy equation, Eq $1$ , for the heat capacity, $c$ .

You have measured all these other quantities in the equation, so you can use them to calculate the heat capacity of antifreeze:

$Δ Q$ [calories]: As described in the purple-highlighted text, This is the number of calories due to one 10-second heat pulse from the first part of Lab 6. There, you measured the average temperature change of water due to one heat pulse, and then used the fact that the heat capacity of water is $c = 1$ calorie/gram/degree C, to figure out how many calories there were in your average heat pulse.
$m$ [grams = milliters]. This is the number of milliliters of anti-freeze you had in your cup. You were told to measure out 100 ml.
$Δ T$ [degrees Celsius]. This was the average temperature change of your antifreeze due to one 10-second heat pulse.

Compare the heat capacity you calculated to the accepted value. The Internet sez that the heat capacity of antifreeze(="ethylene glycol") is 0.58 cal/(g $\cdot$ C $^{o}$ ). Now, that's in terms of grams, but you actually measured it for milliliters (ml). We really ought to use the density of ethylene glycol, 1.11 g/ml, to convert your $c$ (per ml) to $c$ (per gram). But since this is only 10% different, the heat capacity you measured (per ml) should be "fairly close". We would get... $\begin{matrix} (2) & \frac{0.58 cal}{g \cdot C^{o}} \times \frac{1.11 g}{ml} = \frac{0.64 cal}{ml \cdot C^{o}} \end{matrix}$

Mixing hot and cold water

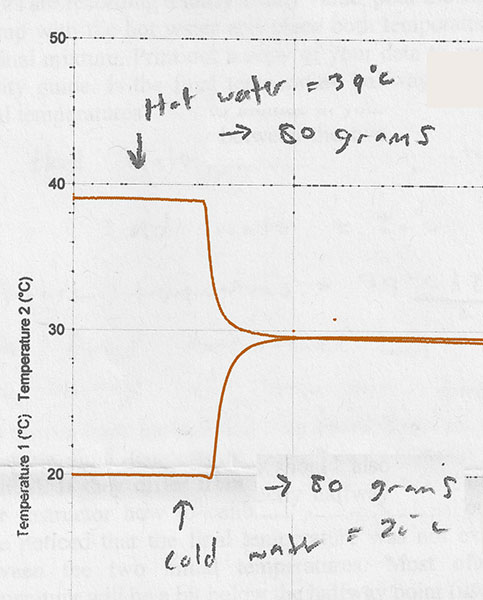You mixed cold and hot water, with this kind of result:

Here's one version of the formula you found for that experiment: $\begin{matrix} (3) & \frac{m_{c}}{m_{f}} T_{c} + \frac{m_{h}}{m_{f}} T_{h} = T_{f} \end{matrix}$

$m_{c}$ is the mass (in grams) of cold water, and $m_{h}$ is the mass of hot water.
$m_{f}$ , the "total mass of water" is $m_{f} = m_{c} + m_{h}$ .
$T_{c}$ was the starting temperature of the cold water and $T_{h}$ was the starting temperature of the hot water.
$T_{f}$ was the final temperature of the mixture of hot and cold water.

The Heat Pulses lab suggests that you try setting the heat energy gained by the cold water equal to the heat energy lost by the hot water, and see if you can solve for $T_{f}$ . Try it! When you solve for $T_{f}$ do you get the same as the expression above, or something different?

Atomic picture of mixing

Lab 5

Start up this simulation of gas properties and go to the diffusion setting. Set it up like this: with red and blue "molecules" of the same weight, but different temperatures.

Try this:

Are all of the particles on the right moving at the same speed?

Are all of the particles on the left moving at the same speed?

By eye, can you estimate which--the particles on the left or on the right--are moving on average faster?

Now "Remove [the] Divider". Watch what happens when a fast particle collides with a slow moving particle. After the collision was the originally-fast particle speeded up or slowed down? What about the originally-slow particle?

About how long does it take until you can no longer tell the difference between the average speed of the red and of the blue particles?

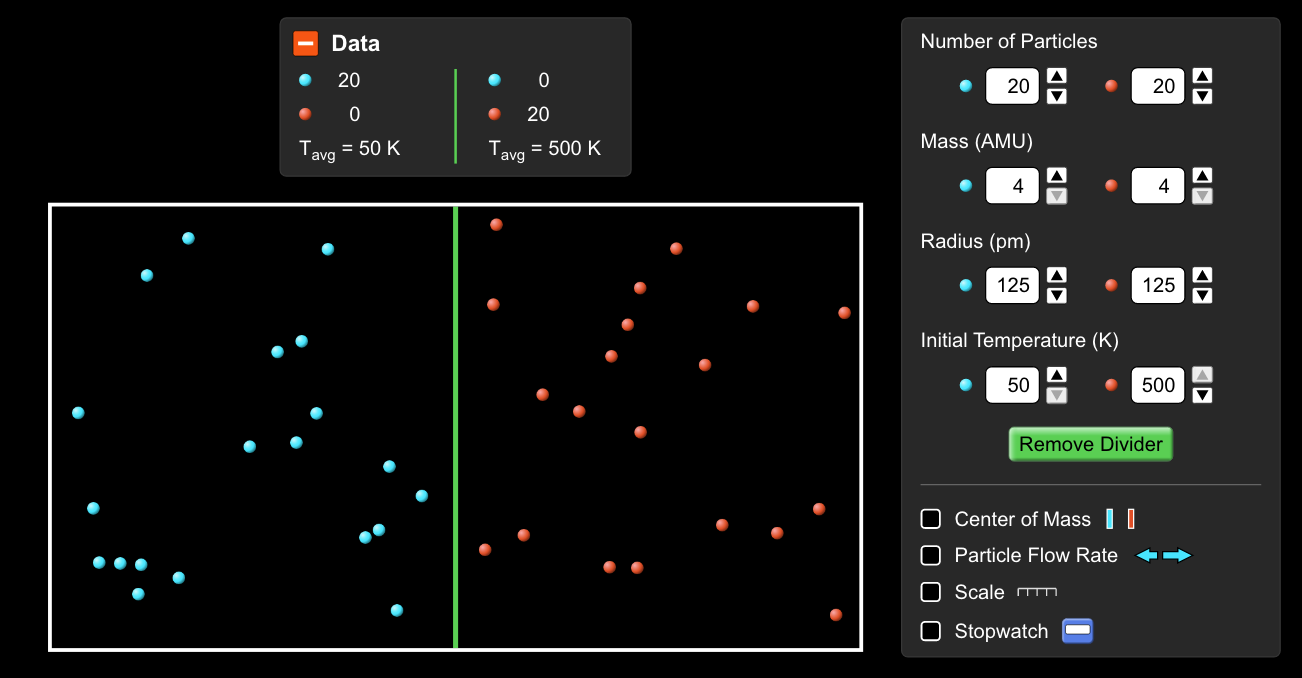
After mixing, the new average speed of molecules is slower than the speed of molecules was in the hot water, but faster than the cold water molecules.